子どもに算数を学ばせたいけれど、何から始めればよいのかわからない、何を目標にすればよいのか分からない、という親御さんは多いのではないでしょうか。
この記事では、4歳までに取り組むべき「数の学び」について、何をどう取り組んだらよいか、わかりやすく解説します。
ぜひ、子どもの算数の土台作りに役立ててください。
子どもの数の知識の習得には順序がある
算数という教科は、それまでに習得した知識を利用して次の新しい知識を学びます。これが他の教科よりも一貫しています。
この性質のため、ある知識を欠いていたり、ある概念の理解が不完全だったりすると、新たな知識の習得や概念の理解が困難になります。
そのため、子どもの数の知識の習得は、発達の順序性を踏まえて、一つ一つ積み上げていく必要があります。
その順序を大まかに示すと、次のようになります。
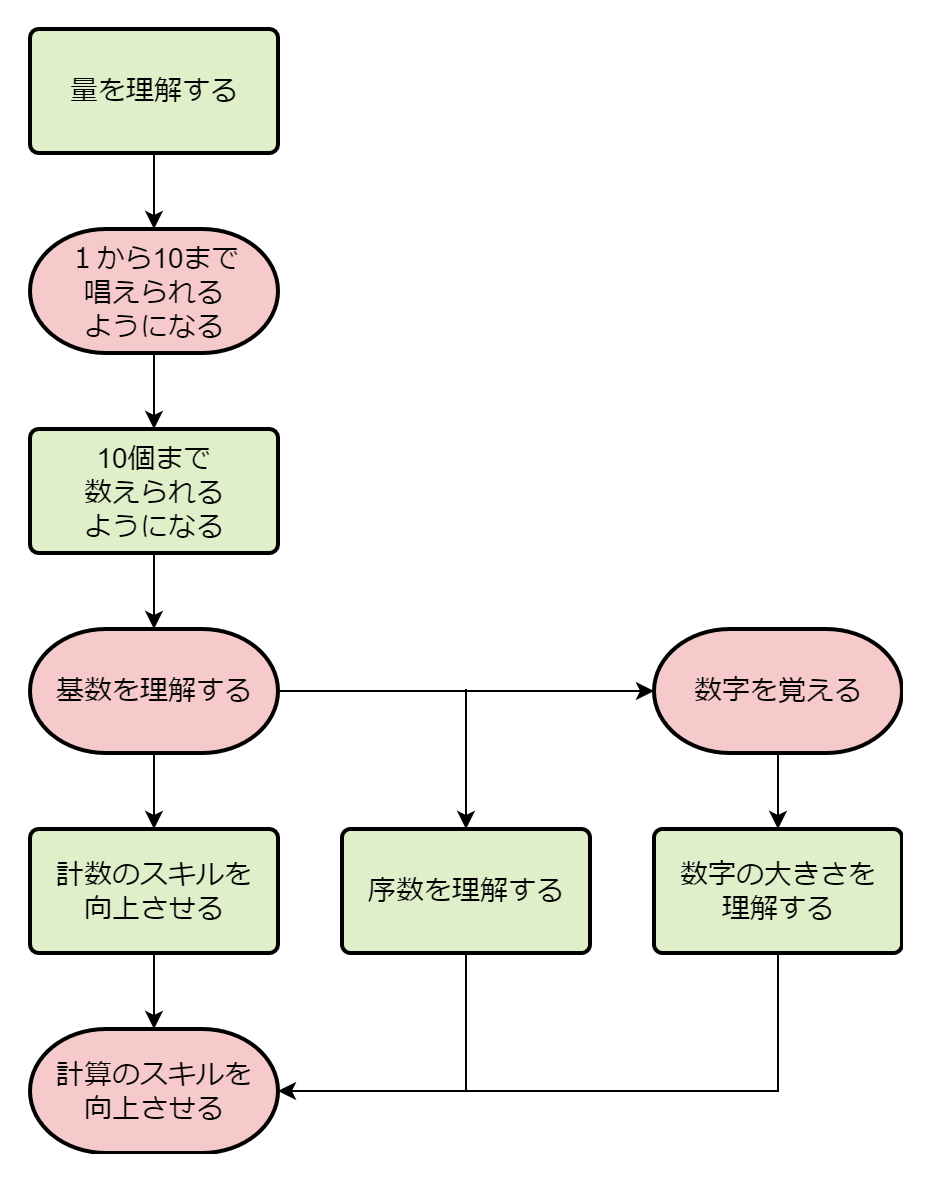
今回の記事では、この図の「基数を理解する」までを取り上げます。
「基数」とは、「集合の要素の数(すなわち、全体の数)」のことです。
ものの順序を表す「序数」は、この対義語になります。
基数の原理を早期に理解するとアドバンテージが得られる
「ものを、いち、に、さん、・・・ と数えて、最後に唱えた数が全体の数を表している」という原理を、「基数の原理」といいます。
4歳までに基数の原理を理解することを目指す
基数の原理は、早い子どもで3歳半ごろ、ほとんどの子どもは4~5歳、遅い子どもでも6歳までには理解します。(01, 02)
幼児の数の学びにおける最初の目標は、この原理をできれば4歳の始めごろ、遅くとも4歳の終りごろまでに理解することです。
というのも、基数の原理を早期に理解した子どもほど、後発の同級生よりも、就学時の数体系の知識レベルが高い傾向にあるからです。(03)
この理解が5歳以降になった子どもの多くは、算数の学習の準備が整わないまま学校生活をスタートさせることになります。
小学校の初めの算数の能力は、その後の学業成績と将来の社会経済的地位の強力な予測因子です。 (04, 05)
また、算数の能力の高い低学年の子どもは、その後の数年間で、努力の源泉となる信念(増大的知能観)を発達させやすいこともわかっています。 (06)
「基数の原理の理解」は、子どもがよりよい将来を手にするためのゲートウェイスキルなのです。
なぜ、基数を早期に理解した子どもほど、就学時の算数のレベルが高いのか?
基数の原理を理解すると、数に関する様々な活動とやり取りが可能になります。
これを早期に達成した子どもほど、就学までの間に、より多くの数的な活動を経験することができます。
また、そのような子どもの多くは、すでに良好なニューメラシー環境にいるはずです。
このような理由から、数の知識とスキルの発達が順調に進むのだと思われます。
基数を理解するまでのステップ
それでは、子どもが基数を理解するまでのステップを一つ一つ見ていきましょう。
1.量を理解する
子どもは、数を理解する前に、「量」を理解します。その量が区切られて個物的に捉えられるようになることから、数の概念が生まれてくるといわれています。(07)
子どもの量の理解は、親などが発する「量に関する言葉」を、目の前にある量と参照することによって促進されます。
「量に関する言葉」とは、「多い・少ない、大きい・小さい、高い・低い」、「もっと」、「増えた・減った」などの言葉をいいます。
子どもが2歳にもなったら、次のような発話を日ごろから意識して行い、量の理解を促していきましょう。
- (チョコレートを割って)「大きいほうをあげるね、はい」
- (積み木遊びで)「どっちが高く積めるかな」、「お父さんのほうが高いぞ」
- (子どもの髪の毛を触って)「だいぶ長くなったね、切ってあげるね」
- (飲料をコップに半分ぐらい注いで)「もっと要る?」
2.数を唱える
子どもの数の理解は、「いち、に、さん、・・・・」と唱えることから始まります。
通常、このステップは2~3歳で達成され、次の2年間で、数詞が表す大きさを理解していきます。(たとえば、01, 08)
数を唱える練習は、行為の始まりや終わりを利用して行います。
たとえば、お風呂から出るときに、「10まで数えてから出ようね」などと言って、一緒に「いち、に、さん、よん、ご、…」と唱えます。
そうやって、できれば3歳のはじめぐらいまでに、10まで唱えられるようにしておきます。
なお、10まで唱えられるようになったあとも、数を唱える練習は続けてください。
20、30と唱えられる数の範囲を段階的に増やしていき、就学までには少なくとも100まで唱えられるようにしておきましょう。
このとき、「じゅういち、じゅうに、じゅうさん、…」と一の位が「いち、に、さん、・・」と進んでいくこと、十の位も「じゅう、にじゅう、さんじゅう、…」と同じ規則で進んでいく(なぜか10だけは「いち」が省略される)ことに早めに気づかせると、数唱、ひいては十進法の理解がスムーズに進展します。
また、子どもが30ぐらいまで唱えられるようになったら、「じゅう、きゅう、はち、なな、ろく、ご、よん、さん、に、いち」と降順に唱える練習も取り入れていきます。
「数え引き」という計算方略の習得に、この逆唱が必要になります。
3.ものを数える(計数)
数が唱えられるようになると、その範囲でものを数えることが可能になります。そうなったら、日常のやりとりの中に、計数を取り入れていきます。
たとえば、おやつをあげるときに、「1個、2個、3個」と数えながら手渡したり、絵本を読み聞かせるときに、挿絵を指しながら「おさるさんが、1匹、2匹、3匹いるね」などと数えたりします。
あるいは、キャンディーなどをいくつか並べて、一緒に数えたり、数えてもらったりします。
数え方は、数える対象の一つ一つを指でさしながら、「いち、に、さん、・・」と数詞を割り振っていきます。
このとき、飛ばしや重複があってはいけません。
「一対一対応」といって、計数を習得するための第一歩となります。
数える個数は、段階的に増やしていき、遅くとも3歳のうちに10まで数えられるようにしておきます。
その間、子どもが「いち、に、さん、…」と数えたあとに、「全部で何個?」と尋ねても、正しい答えが返ってこないかもしれません。
しかし、心配は無用です。
「基数の原理」は、ものを数えられるようになったあと、日常の数に関する会話ややり取りを通して、徐々に理解していきます。
4.基数を理解する
子どもが計数を習得したら、いよいよ基数を理解する段階です。
基数の理解の促し方
基数の理解を促すほとんど唯一の手段は、親の数に関する発話です。
親の発話量と子どもの基数の理解の間には、非常に強固な関係が確認されています。(たとえば、09, 10, 11)
そのため、日常の様々な機会を利用して、「基数」を取り上げていくことが必要になります。
日常の様々な機会を利用して、「基数」を取り上げる
まずは、ものを数える行為が、個数を把握するための行為であることの理解を促していきます。
たとえば、子どもと一緒にものを数えるとき、「いくつあるかな?」と前置きしたり、数えたあとに「全部で4個あるね」などと個数を口にしたりします。
計数のところで紹介した、おやつを「1個、2個、3個」と数えながら手渡したり、絵本の挿絵を指しながら「1匹、2匹、3匹いるね」などと数えたりするやり方も、これを意識したものです。
その次の段階では、個数を直接問題にします。
たとえば、「(キャンディーを渡して)いくつある?」と尋ねたり、「(絵本を見ながら)この中におさるさんは何匹いる?」と尋ねたりして、具体物を数詞に置き換える練習をします。
それと並行して、「お母さんにも一つちょうだい」、「(ティッシュを)2枚とって」などとものの数量を指定して数詞を具体物に置き換える練習もしていきます。
このように、様々な機会を利用して、会話ややりとりに基数を組み込んでいきます。
このとき、子どもが3を理解したら、4、5を、4を理解したら6を導入するといった具合に、常に子どもの理解レベルよりも少し大きい数を取り入れるようにします。
そうやって、遅くとも4歳の終わりまでに、少なくとも6個までの個数が、数えて把握できるようにしておきます。
なぜ6個かというと、4歳で6までの基数値が理解できているかどうかが、就学時の数の知識とスキルの到達度に大きく影響することがわかっているからです。(03)
子どもが基数を理解しているかどうかを確認する方法
子どもが基数を理解しているかどうかは、簡単に確認できます。
キャンディーなどの入った袋を手渡し、「3個ちょうだい」などと言って、指定した個数を取り出してもらいます。
これを、1から6個をランダムに指定して数回行い、全ての試行で正しく取り出すことができたなら、基数を理解していると判断できます。
基数の理解が遅れていたら
子ども基数の理解が遅れている場合は、どうすればよいのでしょうか。
先に、「4歳での基数の理解が就学時の学力を予測する」といいましたが、それはあくまでも、その子がずっと同じニューメラシー環境にいた場合の話です。
この遅れは、日常のニューメラシー活動の質と量を高めることや、親の直接指導によって取り戻すことができます。(12, 13, 14)
やるべきことは、日常の数に関する会話ややり取りを最大化すること、数的な遊びや活動にできるだけ多く従事させることです。
親にそのような意識が根付き、それが日常化すると、子どもの能力は加速的に伸びていきます。
基数の理解の早期達成を目指すことの意味としては、むしろこちらのほうが大きいのかもしれません。
実践あるのみです。
カウンティングにはじまり、基数の理解、数字の大きさの理解、数の合成分解やたし算・引き算まで、幼児期を通して数の学習に利用できるコスパ最強の玩具(教具)です。➔ 活用のし方はこちら
まとめ
●幼児の数に関する学びでは、「基数の原理」を理解することが最初の目標となる。
●「基数の原理」を早期に理解すると、のちの学業や職業に向けて、大きなアドバンテージが得られる。
●「基数の原理」の理解が遅れているからといって、あせる必要はない。日々の数的活動のあり方を改善することで、追いつくことができる。
●逆に、「基数の原理」を早期に達成したからといって、安心してはいけない。数に関する親の発話や活動機会の減少は、子どもの数的発達の鈍化、遅れにつながる。
4歳からの数の学びについてはこちらをお読みください。↓↓
- Wynn, K. (1990). Children’s understanding of counting. Cognition, 36(2), 155–193.
- Knudsen, B., Fischer, M. H., Henning, A., & Aschersleben, G. (2015). The development of Arabic digit knowledge in 4- to 7-year-old children. Journal of Numerical Cognition, 1, 21–37.
- Geary D. C., van Marle K., Chu, F. W., Rouder J., Hoard M. K., & Nugent L. (2018). Early conceptual understanding of cardinality predicts superior school-entry number-system knowledge. Psychological Science, 29(2), 191–205.
- Watts, T. W., Duncan, G. J., Siegler, R. S., & Davis-Kean, P. E. (2014). What’s past is prologue: Relations between early mathematics knowledge and high school achievement. Educational Researcher, 43: 352–360.
- Ritchie, S. J., & Bates, T. C. (2013). Enduring Links From Childhood Mathematics and Reading Achievement to Adult Socioeconomic Status. Psychological Science, 24(7):1301–1308.
- Gunderson, E. A., Park, D., Maloney, E. A., Beilock, S. L., & Levine, S. C. (2018). Reciprocal relations among motivational frameworks, math anxiety, and math achievement in early elementary school. Journal of Cognition and Development, 19:1, 21-46.
- 森 毅 (1989). 数の現象学. 朝日選書.
- Levine, S. C., Suriyakham, L. W., Rowe, M. L., Huttenlocher, J., & Gunderson, E. A. (2010). What counts in the development of young children’s number knowledge? Developmental Psychology, 46:1309–1319.
- Levine, S. C., Suriyakham, L. W., Rowe, M. L., Huttenlocher, J., & Gunderson, E. A. (2010). What counts in the development of young children’s number knowledge? Developmental Psychology, 46:1309–1319.
- Gunderson, E. A., & Levine, S. C. (2011). Some types of parent number talk count more than others: Relations between parents’ input and children’s cardinal-number knowledge. Developmental Science, 14, 1021–1032.
- Susperreguy, M. I., & Davis-Kean, P. E. (2016). Maternal math talk in the home and math skills in preschool children. Early Education and Development, 27, 841–857.
- Watts, T. W., Duncan, G. J., Siegler, R. S., & Davis-Kean, P. E. (2014). What’s past is prologue: Relations between early mathematics knowledge and high school achievement. Educational Researcher, 43: 352–360.
- Honore, N., & Noel, M.-P. (2016). Improving preschoolers’ arithmetic through number magnitude training: The impact of non-symbolic and symbolic training. PLoS ONE, 11(11), e0166685.
- Scalise, N. R., Daubert, E. N., & Ramani, G. B. (2018). Narrowing the early mathematics gap: A play-based intervention to promote low-income preschoolers’ number skills. Journal of Numerical Cognition, 3, 559–581.






子どもの学びに関する多くの学術的知見を持っています。
また、6歳児から中高校生まで勉強を教えた経験があり、学力に与える学習の効果は、年齢が低いほど大きいことを痛感しています。
これらを生かして、効果的で再現性の高い子どもの学びのあり方や方法を提案していきます。よろしくお願いします。