この記事では、百玉そろばんを使った「たし算」と「ひき算」のやり方を解説します。
この記事がカバーする計算の範囲は、次のとおりです。
・1けたの数 + 1けたの数(繰り上がりなし)
・1けたの数 - 1けたの数
・1けたの数 + 1けたの数(繰り上がりあり)
・2けたの数 - 1けたの数(繰り下がりあり)
※ 使用する百玉そろばんは、5玉づつ色分けされているものを推奨しています。ここで採用している計算方略のいくつかは、その特性を利用しています。
繰り上がりのないたし算
基本のたし方
【4+3の場合】
その1 数えたし(まずは、これから)
➊ 4個と3個をセットする。

➋ 上の4個に、下の3個を1個づつ加える。
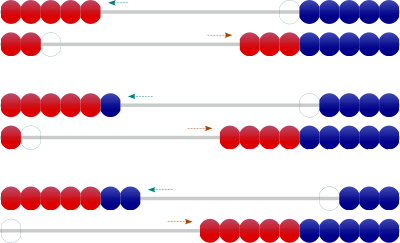
- 「まず、1個を上に持っていくよ」などと言って、下の玉を1個右に寄せ、続けて上の右の玉を1個左に寄せ、「ご」と唱える。
- 同様に、残りの2個を順に移動させながら、「ろく」、「なな」と唱える。
- 慣れてきたらこの手順を連続的に行う。➔「ご、ろく、なな」と数え足して「7」
その2 5のまとまりを意識した方略(推奨)
➊ その1と同じ
➋ 上の4個に、下の3個のうちの1個を加え5個にする。

「まず、1個足して5」
➌ 残りの2個を加える。

「残りの2個を足して7」
※ ➋の時点で、すでに5個と2個の形になっているので、➌の操作は省略してもよいです。➋の形から「5と2で7」と、個数を把握できます。

「5のまとまりを意識した方略」は、数構成の理解の促進、計算方略の拡張の点で優れています。「数えたし」の途中で➋の形になるので、そこからこの方略に導いてあげましょう。
その3 数の構成を意識した方略
➊ その1と同じ
➋ 上の4個に、下の3個をまとめて加える。

「4個に3個を足して7」(個数は玉の色から視覚的に把握する)
百玉そろばんの足し算の操作について、最初は、「なぜ上と下の両方の玉を動かすのだろう?」と疑問に思う子どもがいます。
そのような場合は、右側半分をハンカチなどで隠すと(教示者は裏側から操作する)、下の玉が上に移動するように見えるので、理解しやすくなります。
どちらか一方の数が5のとき
➊ 5個と3個をセットする。
【5+3の場合】

(この形のまま)「5と3で8」
最初から「5個と3個」の形になっているので、わざわざ動かす必要はありません(5個と3個の並び方が、縦から横に変わるだけです)。
「基本のたし方 その2- ➌」と同じです。
小さい数に大きい数を足すとき
【2+7の場合】
その1 前の数に足す(上の列に足す)
➊ 2個と7個をセットする。

➋ 上の2個に、下の7個を加える。

たし方は、「基本のたし方-その1,その2,その3」にしたがう。
その2 大きいほうの数に足す(下の列に足す)
➊ その1と同じ
➋ 下の7個に、上の2個を加える。

「はち、きゅう」と数え足して「9」
または、
2個をまとめて足して「7と2で9」

小さい数に大きいと数を足すときは、「その2」のように足し方を逆にすると、計算(操作)が容易になることが多いです。二つの方法のどちらがやりやすいか、いろいろな数の組み合わせで比べてみるとよいです。
前に足すか後ろに足すか?
「被加数 < 加数」のとき、後ろに足すことのメリットとしては、次の二つがあげられます。
大きい数に小さい数を足すほうが、計算が容易
特に、1+6、2+6、3+6、1+7、2+7、1+8のように、二つの数の差が大きいときは、後ろに足す方が計算しやすいです。
一方、3+4のように二つの数の差が小さいときは、どちらに足しても大きな違いはないかもしれません。
2色の百玉そろばんでは、大きい数に小さい数を足すほうが、視覚的に数の構成を理解しやすい
たとえば、2+7の場合、2個に7個を加えるよりも(左図、スマホでは上図)、7個に2個を加えるほうが(右図、スマホでは下図)、「7と2と9」の関係、あるいは「5と2と2と9」の関係が理解しやすいです(つまり、数構成のインプットや、数感覚を養うのに効果的です)。
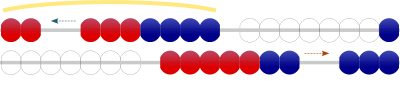
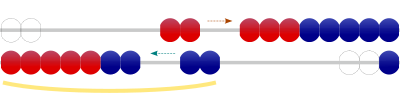
デメリットとしては、加えられる数と加える数が逆になるので、操作が式本来の意味と一致しないことです(ただし、「足し合わせる」という意味の場合は矛盾しません)。
一方で、2に7を足せるようにしておくことにも、意味はあります。
たとえば、「82+7」のような記号数の計算では、「7に2を足して9、80と9で89」とやってもよいのですが、「82の2に直接7を足す」ほうが数の操作がシンプルになります。
繰り下がりのないひき算
基本のひき方
【7-3の場合】
その1 数えひき(まずは、これから)
➊ 7個と3個をセットする。

下の列は、ひく数(あといくつ引くか)を確認するためのものです(図は、3個引くことを表しています)。
➋ 7個から3個を1個づつ取り去る。
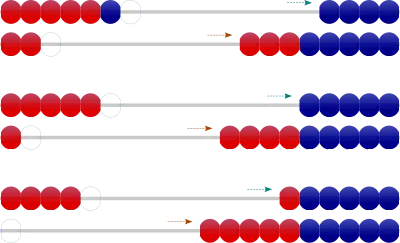
- 「まず、1個とるよ」などと言って、7個の端の1個を右に寄せ、「ろく」と唱える。下の列の玉も、引いた分は右に戻しておく。
- 同様に、残りの2個を順に移動させながら、「ご」、「よん」と唱える。
- 慣れてきたらこの手順を連続的に行う。➔「ろく、ご、よん」と数え引いて「4」
その2 5のまとまりを意識した方略(推奨)
➊ その1と同じ
➋ まず、2個を右に移動させて5個にする。

「まず、2個取って5」
➌ 残りの1個を右に移動させる。

「残りの1個を取って4」
その3 数の構成を意識した方略
➊ その1と同じ
➋ 7個のうちの3個を右に移動させる。

「7個から3個を取って4」(個数は視覚的に把握する)
ひく数が5のとき
【8-5の場合】
「8」を「5(赤のかたまり)」と「3」に分解し、5を取り除きます。
「基本の引き方」でもよいのですが、こちらのほうがシンプルで、数構造の理解に役立ちます。
➊ 8個と5個をセットする。

➋ 8個を5個と3個に切り分ける。

「(赤い玉を指して)ここに5個のかたまりがあるけれど、動かせないからこうするね」などと言って、色の境界で玉を切り離す。➔ (青い玉を見て)「3」
5個のまとまりに注目したやり方です。玉の動きが実際の計算と逆になりますが、最初は赤の5個を手で隠すと、子どもは理解しやすいです。

繰り下がりのないひき算で5を引くときは、引かれる数を「5といくつ」に分解すると、簡単に計算できます。この考え方は暗算にもそのまま適用できます。
ひく数とひかれる数の差が小さいとき
【9-8の場合】
ひく数とひかれる数の差が小さいとき(差が1か2か3のとき)は、上の列の玉と下の列の玉を対応させるやり方が理解しやすいです。
操作手順は「5をひくとき」と同じです。
この方略は、補加法や個数差の理解につながります。
➊ 9個と8個をセットする。

➋ 9個を8個と1個に切り分ける。

(青い玉を見て)「1」
繰り上がりのあるたし算
基本のたし方
【8+4の場合】
➊ 8個と4個をセットする。

➋ 上の8個に、下の4個のうちの2個を加えて10個にする。

「上に2個持っていくよ」と言って、下の玉を2個右に寄せ、次に上の右の玉を2個左に寄せる。➔「10と2で12」
どちらか一方の数が5のとき
【7+5の場合】
最初から「10個(5個と5個)と2個」の形になっているので、わざわざ動かす必要はありません。
普通に足してもよいのですが、こちらのほうが数構造的にシンプルです。
➊ 7個と5個をセットする。

(この形のまま)「5と5で10、10と2で12」

一方の数が5のときは、5のまとまりどうしを足すと、簡単に計算できます。この考え方は暗算にもそのまま適用できます。
6+6,6+7,7+6,7+7の場合
【7+6の場合】
その1 基本の足し方
➊ 7個と6個をセットする。

➋ 上の7個に、下6個のうちの3個を加えて10個にする。

「(10と3で)13」
その2 5のまとまりを利用する方略
足し合わせる数をそれぞれ「5といくつ」に分解し、「10(5と5)といくつ」という見方をします。
この方略が適しているのは、5の端数(図の青い玉の個数)の合計が4ないし5以下のときです。
5個ぐらいからサビタイジング(視覚的な個数把握)が難しくなるのと、数構造的にメリットが薄れます。
➊ その1と同じ
➋ (➊の形のまま、または赤玉と青玉を少しだけ切り離す)

「10(5と5)と3(2と1)で13」

6+6,6+7,7+6,7+7,6+8,8+6などで、その1、その2のやり方を比べてみるとよいです。なお、その1、その2とも暗算にそのまま適用できます。
小さい数に大きい数を足すとき
【3+9の場合】
その1 前の数に足す(上の列に足す)
➊ 3個と9個をセットする。

➋ 上の3個に、下の9個のうちの7個を加える。

「(10と2で)12」
その2 大きいほうの数に足す(下の列に足す)
➊ その1と同じ
➋ 下の9個に、上の3個のうちの2個を加える。

「(2と10で)12」
「その1」のように、「A(被加数)+B(加数)」のBを分解してAに足すやり方を「加数分解」、「その2」のように、Aを分解してBに足すやり方を「被加数分解」といいます。

小さい数に大きいと数を足すときは、足し方を逆にすると(その2)、簡単に計算(操作)できる場合が多いです。二つの方法のどちらがやりやすいか、いろいろな数の組み合わせで比べてみるとよいです。
繰り下がりのあるひき算
基本のひき方(減減法と減加法)
【14-8の場合】
その1 減減法
➊ 14個と8個をセットする。
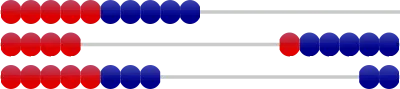
3列目は、引く数(あといくつ引くか)を確認するために設けています。
➋ まず、端数をとって10個にする。
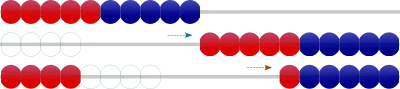
「まず、4個取って10」
➌ 残りを10個から取る。

「残りの4個をとって6」
その2 減加法
➊ その1と同じ
➋ 上の列の10個から8個をとる。
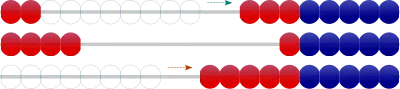
「2と4で6」
減減法か減加法か?
くり下がりのあるひき算で、減減法を用いるか、減加法を用いるかは、数の組み合わせしだいです。
たとえば、13-4なら減減法、11-9なら減加法、16-8ならどちらでも大差ない、という判断になるかもしれません。
一般に、「13-4のように、引かれる数の一の位の数と引く数の差が小さいときは減減法がやりやすく、13-9のように、引く数が10に近いときは減加法がやりやすい」という傾向はありますが、「これが正解」というのはありません。
「2けた-1けた」の繰り下がりのあるひき算の全パターンを10人にやらせたら、どの計算に減減法を用いるか、また減加法を用いるか、全てが一致する人はいないでしょう。
重要なのは、百玉そろばんであれ、記号数の計算であれ、その都度試して、どちらがやりやすいか比べてみることです。
このように、「方略を比較して、よりよい方略を選択する」ことは、数構成に対する理解を深め、数学に必要とされる「ナンバーセンス」を育むことにつながるからです。




子どもの学びに関する多くの学術的知見を持っています。
また、6歳児から中高校生まで勉強を教えた経験があり、学力に与える学習の効果は、年齢が低いほど大きいことを痛感しています。
これらを生かして、効果的で再現性の高い子どもの学びのあり方や方法を提案していきます。よろしくお願いします。